Google Ads
Module 9.1
LCR Series Circuit Action
- Recognise LCR Series circuits and describe their action using phasor diagrams and appropriate equations:
- • Below Resonance
- • Above Resonance
- • At Resonance
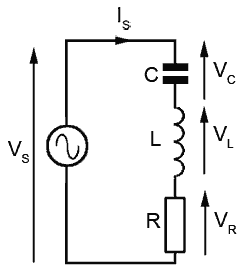
Fig. 9.1.1 LCR Series Circuit.
The circuit in Fig 9.1.1 contains all the elements so far considered separately in modules 1 to 8, namely inductance, capacitance and resistance, as well as their properties such as Reactance, Phase, Impedance etc.
This module considers the effects of L C and R connected together in series and supplied with an alternating voltage. In such an arrangement, the same circuit current (I) flows through all the components of the circuit, and VR VL and VC indicate the voltages across the resistor, the inductor and the capacitor respectively.
Module 6.1 described the effect of internal resistance on the voltage measured across an inductor. In LCR circuits both internal (inductor) resistance, and external resistance are present in the complete circuit. Therefore, it will be easier to consider that the voltage VR is the voltage across the TOTAL circuit resistance, which comprises the internal resistance of L, added to any separate fixed resistor. Where VS is mentioned, this is the applied supply voltage.
The phase relationship between the supply voltage VS and the circuit current IS depends on the relative values of inductance and capacitance, and whether the inductive reactance (XL) is greater or less than the capacitive reactance (XC). There are various conditions possible, which can be illustrated using phasor diagrams.
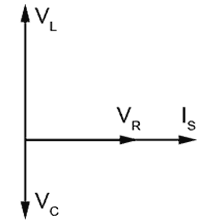
Fig 9.1.2 Phasors for VL and VC are in anti phase.
Fig 9.1.2 shows the circuit conditions when the inductive reactance (XL) is greater than the capacitive reactance (XC). In this case, since both L and C carry the same current, and XL is greater than XC, it follows that VL must be greater than VC.
(VL = ISXL and VC = ISXC).
Remember that VC and VL are in anti-phase to each other due to their 90° leading and lagging relationship with the circuit current (IS). As VL and VC directly oppose each other, a resulting voltage is created, which will be the difference between VC and VL. This is called the REACTIVE VOLTAGE and its value can be calculated by simply subtracting VC from VL. This is shown in Fig 9.1.3 by the phasor (VL − VC).
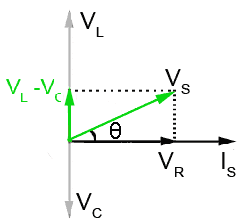
Fig 9.1.3 VL is greater than VC so the circuit behaves like an inductor
The length of the phasor (VL − VC) can be arrived at graphically by removing a portion from the tip of the phasor (VL), equivalent to the length of phasor (VC).
VS is therefore the phasor sum of the reactive voltage (VL − VC) and VR. The phase angle θ shows that the circuit current IS lags on the supply voltage VS by between 90° and 0°, depending on the relative sizes of (VL − VC) and VR. Because IS lags VS, this must mean that the circuit is mainly inductive, but the value of inductance has been reduced by the presence of C. Also the phase difference between IS and VS is no longer 90° as it would be if the circuit consisted of only pure inductance and resistance.
Because the phasors for (VL − VC), VR and VS in Fig 9.1.3 form a right angle triangle, a number of properties and values in the circuit can be calculated using either Pythagoras´ Theorem or some basic trigonometry, as illustrated in "Using Phasor Diagrams" in Module 5.4.
For example:
VS2 = (VL − VC)2 + VR2
or
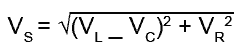
The total circuit impedance (Z) can be found in a similar way:
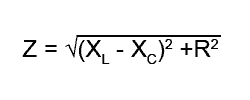
The phase angle between (VL − VC) and VR can be found using trigonometry as illustrated in "Using Phasor Diagrams" in Module 5.4.
tanθ = opposite ÷ adjacent,
therefore
tanθ = (VL − VC) ÷ VR
so to find the angle θ
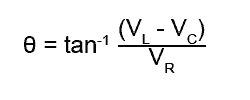
Also, Ohms Law states that R (or X) = V/I
Therefore if (VL − VC) and VR are each divided by the current (IS) this allows the phase angle θ to be found using the resistances and reactances, without first working out the individual voltages.
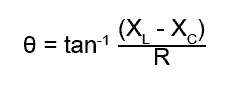
This can be useful when component values need to be chosen for a series circuit giving a required angle of phase shift.
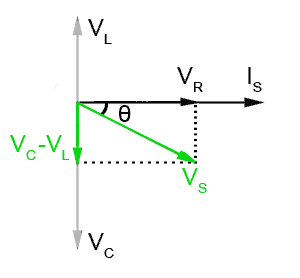
Fig 9.1.4 When VC is larger than VL the circuit is capacitive.
Fig 9.1.4 illustrates the phasor diagram for a LCR series circuit in which XC is greater than XL showing that when VC exceeds VL the situation illustrated in Fig 9.1.3 is reversed.
The resultant reactive voltage is now given by (VC − VL) and VS is the phasor sum of (VC − VL) and VR.
The phase angle θ now shows that the circuit current (IS) leads supply voltage (VS) by between 0° and 90°. The overall circuit is now capacitive, but less so than if L was not present.
In using the above formulae, remember that the reactive value (the difference between VL and VC or XL and XC) is given by subtracting the smaller value from the larger value. For example, when VC is larger than VL:
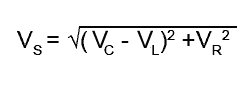
Looking at the phasor diagrams for a LCR series circuit it can be seen that the supply voltage (VS) can either lead or lag the supply current(IS) depending largely on the relative values of the component reactances, XL and XC.
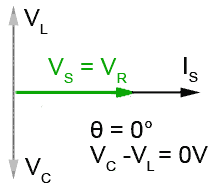
Fig 9.1.5 When VL and VC are equal the circuit is purely resistive.
As shown in Module 6.1 and 6.2, the reactance of L and C depends on frequency, so if the frequency of the supply voltage VS is varied over a suitable range, the series LCR circuit can be made to act as either an inductor, or as a capacitor, but that's not all.
Fig 9.1.5 shows the situation, which must occur at some particular frequency, when XC and XL (and therefore VC and VL) are equal.
The opposing and equal voltages VC and VL now completely cancel each other out. The supply voltage and the circuit current must now be in phase, so the circuit is apparently entirely resistive! L and C have completely "disappeared". This special case is called SERIES RESONANCE and is explained further in Module 9.2.


