Google Ads
Module 9.3
Voltage Magnification
- • Describe voltage magnification and Q factor in Series LCR Circuits.
- • Calculate Voltage Magnification using appropriate formulae.
In the answers to the calculations in example 9.2.2 it should be noticeable that, at the circuit´s resonant frequency ƒr of 107kHz, the reactive voltages across L and C are equal and each is greater than the circuit supply voltage VS of 100V.
This is possible because, at resonance the voltage (VC = 199.56V) across the capacitor, is in anti−phase to the voltage (VL = 199.56V) across the inductance. As these two voltages are equal and opposite in phase, they completely cancel each other out, leaving only the supply voltage developed across the circuit impedance, which at resonance is the same as the total resistance of 320 + 18 = 338Ω.
At the resonant frequency the current through the circuit is at a maximum value of about 296mA. Because of the anti phase cancelling effect at resonance, the two reactive voltages VC and VL have "disappeared"! This leaves the supply current IS effectively flowing through R and the inductor resistance RL in series.
In this example the effect of the inductor´s 18Ω internal resistance on VL is so small (0.03V) as to be negligible and VL TOT is the same value as VL at approximately 199.6V..
As the total circuit impedance is less than either the capacitive or inductive reactances at resonance, the supply voltage of 100V (developed across the circuit resistance) is less than either of the opposing reactive voltages VC or VL. This effect, where the internal component reactive voltages are greater than the supply voltage is called VOLTAGE MAGNIFICATION.
This can be a very useful property, and is used for example in the antenna stages of radio receivers where a series circuit, resonant at the frequency of the transmission being received, is used to magnify the voltage amplitude of the received signal voltage, before it is fed to any transistor amplifiers in the circuit.
The voltage magnification that takes place at resonance is given the symbol Q and the "Q Factor" (the voltage magnification) of LC Band Pass and Band Stop filter circuits for example, controls the "rejection", the ratio of the wanted to the unwanted frequencies that can be achieved by the circuit.
The effects of voltage magnification are particularly useful as they can provide magnification of AC signal voltages using only passive components, i.e. without the need for any external power supply.
In some cases voltage magnification can also be a dangerous property. in high voltage mains (line) operated equipment containing inductance and capacitance, care must be taken during design to ensure that the circuit does not resonate at frequencies too close to that of the mains (line) supply. If that should happen, extremely high reactive voltages could be generated within the equipment, with disastrous consequences for the circuit and/or the user.
The Q factor can be calculated using a simple formula. The ratio of the supply voltage VS to either of the (equal) reactive voltages VC or VL will be in the same ratio as the total circuit resistance (R) is to either of the reactances (XC or XL) at resonance. The ratio of the reactive voltage VL to the supply voltage VS is the magnification factor Q.
The formula for finding Q (the voltage magnification) uses the ratio of the inductive reactance to the total circuit resistance.
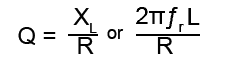
Where XL is the inductive reactance at resonance, given by 2πƒrL and R is the TOTAL circuit resistance. Note that Q does not have any units (volts, ohms etc.), as it is a RATIO


