Google Ads
Module 6.2
Capacitive ReactanceXC
- After studying this section, you should be able to describe:
- •Capacitive Reactance.
- •The relationship between reactance, frequency and capacitance.
- •Graphical representation of capacitive reactance.
In a capacitor with direct voltage applied, module 4.2 showed that the current flow falls to zero after the initial transient period. When an alternating voltage of any appreciable frequency is applied however, current flows first in one direction, and then the other. The capacitor is first charging, and then discharging, so provided that the frequency of the applied AC is high enough, the capacitor never reaches its fully charged, zero current state in either polarity, and current continues to flow all the time. The amount of current flowing will depend on the angular velocity of the applied voltage, and on the capacitance of the capacitor
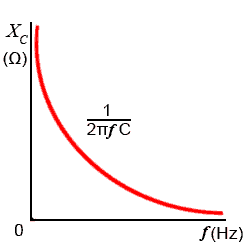
Fig 6.2.1 Capacitive Reactance XC
The lower the frequency of the applied voltage, the more time the capacitor has to reach the fully charged, zero current state before the voltage reverses its polarity and begins to discharge the capacitor again. The capacitor therefore spends more time fully charged and passing much less current, the average value of current flow is therefore less at low frequencies. When a higher frequency is applied, the capacitor changes from charging to discharging sooner in its charge curve and it remains further from its fully charged state. As a consequence, more current flows. The opposition to current flow in any capacitor of a given size therefore reduces as frequency increases. This frequency dependent opposition to current flow in a capacitor is called CAPACITIVE REACTANCE (XC). The formula for capacitive reactance is:
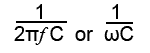
Fig 6.2.1 shows a graph of capacitive reactance against frequency for a given value of capacitor, with capacitive reactance (XC) inversly proportional to frequency, (XC reducing as frequency increases).
Reactance is also inversely proportional to the value of capacitance, and the value of XC at any one particular frequency will be less in larger capacitors than in smaller ones. All capacitors will have infinitely high values of reactance at 0Hz, (i.e. no current flows at dc), but in large capacitors, the reactance falls to a low level at much lower frequencies than in smaller capacitors. For this reason larger capacitors are used in low frequency applications.


