Google Ads
Module 11.1
Transformer Operation
- After studying this section, you should be able to describe:
- • Basic transformer operation.
- • Turns ratio.
- • Power ratio.
- • Transformation ratio.
- • Transformer losses: Copper, Hysteresis & Eddy current.
- • Transformer efficiency and off load current.
Transformers.
A transformer uses the principles of electromagnetism to change one A.C. voltage level to another. Faraday's work in the 19th century showed that a changing current in a conductor (e.g. a transformer primary winding) sets up a changing magnetic field around the conductor. If another conductor (secondary winding) is placed within this changing magnetic field a voltage will be induced into that winding.
Turns Ratio.
Faraday also calculated that the voltage induced into the secondary winding would have a magnitude that depends on the TURNS RATIO of the transformer. i.e. If the secondary winding has half the number of turns of the primary winding, then the secondary voltage will be half the voltage across the primary winding. Likewise, if the secondary winding has twice the number of turns of the primary winding, the secondary voltage will be double the primary voltage.
Power ratio.
Because the transformer is a passive component, (it has no external power supply) it cannot produce more power out from its secondary than is applied to its primary. Therefore if the secondary voltage is greater than the primary voltage by a particular amount, the secondary current will be smaller than the primary current by a similar amount, i.e. If the voltage is doubled the current will be halved.
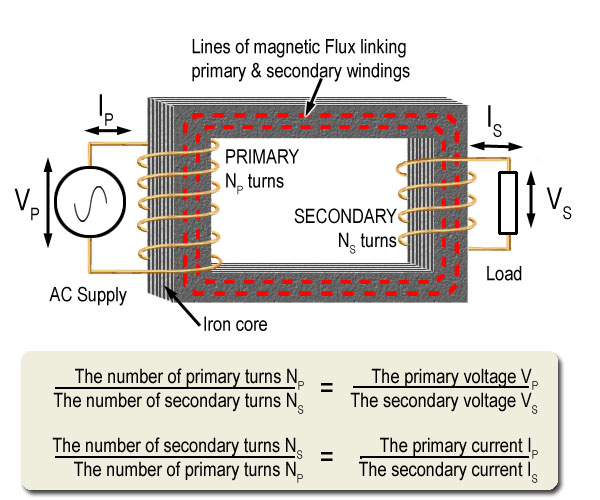
Fig 11.1.1 Basic Transformer Operation.
Transformation Ratio.
Basic Transformer operation can be described by two formulae relating the transformation ratio to the turns ratio of the transformer windings.
- VP = the primary voltage.
- IP = the primary current.
- VS = the secondary voltage.
- IS = the secondary current.
- NP = the number of turns in the primary winding.
- NS = the number of turns in the secondary winding.
Transformer Losses.
The formulae in Fig. 11.1.1 relate to an ideal transformer, i.e. a transformer with no power losses, in which, Primary volt amperes = Secondary volt amperes.
While practical transformers can be extremely efficient, some losses will occur because not all of the magnetic flux produced by the primary winding will link with the secondary winding. The power losses that occur in a transformer are of three types;
1. Copper Losses.
These losses can also be called winding losses or I2R losses, because they can occur in windings made from metals other than copper. The losses become evident as heat, generated in the (copper) wire windings as they dissipate power due to the resistance of the wire.
The power loss in a transformer winding can be calculated by using the current in the winding and its resistance, in formula for power, P = I2R. This formula is the reason copper losses are sometimes called I2R losses. To minimise the losses the resistance of the winding must be kept low, using wire of suitable cross sectional area and low resistivity.
2. Hysteresis losses.
Each time the alternating current reverses (once each cycle), tiny "magnetic domains" within the core material are reversed. These are physical changes within the core material and take up some energy. The amount of energy used depends on the "reluctance" of the core material; in large cores of power transformers where hysteresis loss maybe a problem it is largely overcome by using special low reluctance "grain oriented" steel as the core material.
3. Eddy Current losses.
Because the iron or steel core is an electrical conductor as well as a magnetic circuit, the changing current in the primary will tend to set up an EMF within the core as well as in the secondary winding. The currents induced into the core will oppose the changes of magnetic field taking place in the core. For this reason these eddy currents must be kept as small as possible. This is achieved by dividing the metal core into thin sheets or "laminations" each one insulated from the others by an insulating coat of lacquer or oxide. Laminated cores greatly reduce the formation of eddy currents without affecting the magnetic properties of the core.
Ferrite Cores.
In high frequency transformers eddy current losses are reduced by using a core made of a ceramic material containing a large proportion of tiny metal particles, iron dust or manganese zinc. The ceramic insulates the metal particles from each other, giving a similar effect to laminations, and performing better at high frequencies.
Due to the ways of reducing losses described above, practical transformers closely approach the ideal in performance. In large power transformers, efficiencies of about 98% can be achieved. Therefore for most practical calculations, it can be assumed that a transformer is "Ideal" unless its losses are specified. The actual secondary voltages in a practical transformer will be only slightly less than those calculated using the theoretical transformation ratio.
Off Load Current.
Because the action of a transformer is nearly perfect, the power in both primary and secondary windings is the same, so when no load is put on the secondary, no secondary current flows and the power in the secondary is zero (V x I = 0). Therefore, although a voltage is applied to the primary no current will flow, as the power in the primary must also be zero. In practical transformers the "Off Load Current" in the primary is actually very low.
Volts per Turn.
A transformer with a primary winding of 1000 turns and a secondary winding of 100 turns has a turns ratio of 1000:100 or 10:1. Therefore 100 volts applied to the primary will produce a secondary voltage of 10 volts.
Another way to consider transformer voltages is by volts/turn; if the 100 volts applied to the 1000 turn primary produces 100/1000 = 0.1 volts per turn, then each single turn on the 100 turn secondary winding will produce 0.1V so the total secondary voltage will be 100 × 0.1V = 10V.
The same method can be used to find the values of voltage appearing across individual tappings of an autotransformer when the number of turns per tapping is known.
Simply divide the total voltage across the whole winding by the total number of turns, and multiply this result by the number of turns in the particular tapping.


