Google Ads
Module 4.3
The CR Time Constant
- After studying this section, you should be able to describe:
- • The Time constant of a CR circuit
- ...and carry out calculations involving
- •Time constants in a simple CR circuit.
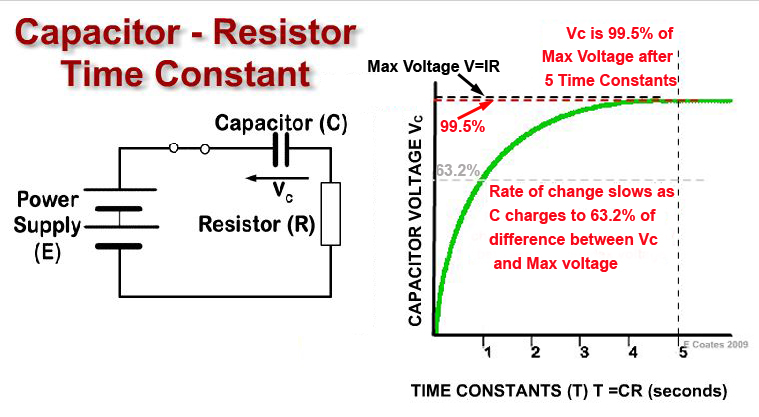
Fig. 4.3.1 The CR Time Constant.
When a voltage is applied to a capacitor it takes some amount of time for the voltage to increase. This increase happens in a curve that follows a mathematically "exponential" law to its maximum value, after which, the voltage will remain at this "steady state" value until there is some other external change to cause a change in voltage. From the instant the voltage is applied, the rate of change of the voltage is high, and if it was to continue in a linear manner, then VC would reach its maximum value in a time equal to one time constant (T), where T (in seconds) is equal to C (in Farads) multiplied by R (in ohms), see fig 4.3.1. above. That is: T = CR
Fully Charged?
After about 5 time constant periods (5CR) the capacitor voltage will have very nearly reached the value E. Because the rate of charge is exponential, in each successive time constant period Vc rises to 63.2% of the difference in voltage between its present value, and the theoretical maximum voltage (VC = E). Therefore the 63.2% becomes a smaller and smaller voltage rise with each time constant period and although, for all practical purposes VC = E in fact VC never quite reaches the value of E.
About the Formula
For this reason the time when VC = E cannot be accurately defined, therefore some other accurate time measurement must be used to define the time it takes for VC to reach some given level. One simple solution would be to say that a time constant will equal the time it takes for VC to reach half the supply voltage. This would work but then the formula for T would not be as easy to remember as CR (or L/R), it would also make calculations involving time constants more difficult. Because time constant calculations are important, and often needed, it is better to make the definition of the time constant (T) in a CR circuit:
THE TIME TAKEN FOR THE VOLTAGE ACROSS A CAPACITOR TO INCREASE BY 63.2% OF THE DIFFERENCE BETWEEN ITS PRESENT AND FINAL VALUES.
a slightly more complicated definition, but this provides a much easier formula to remember and to work with, T = CR.
Discharging C
When the capacitor is discharging the same CR formula applies, as the capacitor also discharges in an exponential fashion, quickly at first and then more slowly. During discharge the voltage will FALL by 63.2% to 36.8% of its maximum value in one time constant period T.


