Amplifier Gain & Decibels
Module 1.3
- After studying this section, you should be able to:
- Describe voltage amplification as a ratio.
- Compare linear and logarithmic scales.
- Describe ratios using the decibel.
- • Positive and negative decibel values.
- • Convert power gain to decibels.
- • Convert voltage gain to decibels.
- • Recognise commonly used dB values.
Voltage Amplification
The Voltage Amplification (Av) or Gain of a voltage amplifier is given by:
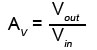
With both voltages measured in the same way (i.e. both RMS, both Peak, or both Peak to Peak), Av is a ratio of how much bigger is the output than the input, and so has no units. It is a basic measure of the Gain or effectiveness of the amplifier.
Because the output of an amplifier varies at different signal frequencies, measurements of output power, or often voltage, which is easier to measure than power, are plotted against frequency on a graph (response curve) to show comparative output across the working frequency band of the amplifier.
Logarithmic Scales
Response curves normally use a logarithmic scale of frequency, plotted along the horizontal x-axis. This allows for a wider range of frequency to be accommodated than if a linear scale were used.

Fig. 1.3.1 Logarithmic and Linear Scales Compared
The vertical y-axis is marked in linear divisions but using the logarithmic units of decibels allowing for a much greater range within the same distance. The logarithmic unit used is the decibel, which is one tenth of a Bel, a unit originally designed for measuring losses of telephone cables, but as the Bel is generally too large for most electronic uses, the decibel (dB) is the unit of choice. Apart from providing a more convenient scale the decibel has another advantage in displaying audio information, the human ear also responds to the loudness of sounds in a manner similar to a logarithmic scale, so using a decibel scale gives a more meaningful representation of audio levels.
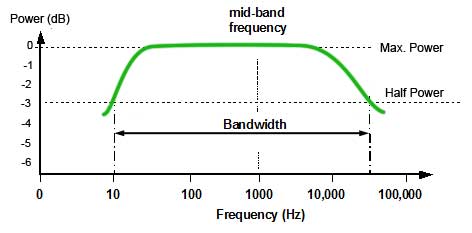
Fig 1.3.2 Audio Power Response Curve
Power Gain in dBs
To describe a change in output power over the whole frequency range of the amplifier, a response curve, plotted in decibels is used to show variations in output. The powers at various frequencies throughout the range are compared to a particular reference frequency, (the mid band frequency). The difference in power at the mid band frequency and the power at any other frequency being measured, is given as so many decibels greater (+dB) or less (-dB) than the mid band frequency, which is given a value of 0dB. Notice that, on the logarithmic frequency scale in Fig 1.3.1 the middle of the 10Hz to 100kHz band is 1kHz and frequencies around this figure (where the output is usually at its maximum) are normally chosen as the reference frequency.
Converting a power gain ratio to dBs is calculated by multiplying the log of the ratio by 10:
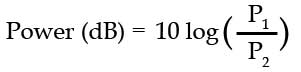
Where P1 is the power at mid band and P2 is the power being measured.
Note:
When using this formula in a calculator the use of brackets is important, so that 10 x the log of (P1/P2) is used, rather than 10 x the log of P1, divided by P2.
e.g. if P1 = 6 and P2 =3
10 x log(6/3) =3dB (right answer), but 10 x log 6/3 = 2.6dB (wrong answer).
Voltage Gain in dBs
Although it is common to describe the voltage gain of an amplifier as so many decibels, this is not really an accurate use for the unit. It is OK to use decibels to compare the output of an amplifier at different frequencies, since all the measurements of output power or voltage are taken across the same impedance (the amplifier load), but when describing the voltage gain (between input and output) of an amplifier, the input and output voltages are being developed across quite different impedances. However it is quite widely accepted to also describe voltage gain in decibels.
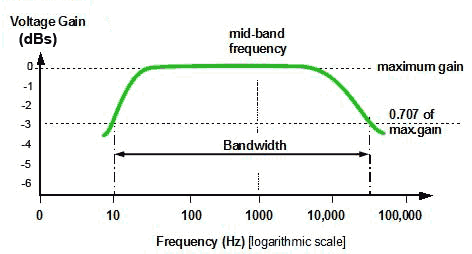
Fig 1.3.3 Audio Voltage Response Curve
When voltage gain(Av) or current gain (Ai) is plotted against frequency the −3dB points are where the gain falls to 0.707 of the maximum (mid band) gain.

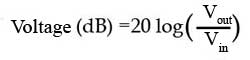
Notice that converting voltage ratios to dBs uses 20 log(Vout/Vin)
Describing the voltage gain of an amplifier that produces an output voltage of 3.5V for an input of 35mV as being 40dB, is equivalent to saying that the output voltage is 100 times greater than the input voltage.
To reverse the process, and convert dBs to a voltage ratios for example, use:
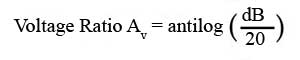
Note that the brackets are important and antilog may be shown on calculator keypads as 10x or 10^ and is also usually Shift +log. Use the same formula for dBs to Current gain ratio, and to convert dBs to a power ratio, simply replace the 20 in the formula with 10.
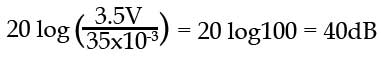
An advantage of using dBs to indicate the gain of amplifiers is that in multi stage amplifiers, the total gain of a series of amplifiers expressed in simple ratios, would be the product of the individual gains:
Av1 x Av2 x Av3 x Av4 ...etc.
This can produce some very large numbers, but the total of individual gains expressed in dBs would be the sum of the individual gains:
Av1 + Av2 + Av3 + Av4 ...etc.
Likewise losses due to circuits such as filters, attenuators etc. are subtracted to give the total loss.
Commonly Encountered dB Values
0dB The reference level to which all +dB and −dB figures refer.
±1dB The least noticeable change in audio levels, also used for the limits of bandwidth on high quality audio amplifiers.
−3dB Commonly used for limits of bandwidth in amplifiers, indicating the points where:
a. The output voltage has fallen to 0.707 of the maximum (mid band) output.
b. The output power has fallen to half the maximum or mid band power.
(Half the VOLTAGE amplitude is −6dB)
Figures often quoted on attenuators designed to reduce the outputs on signal generators by measured amounts.
−20 dB Signal voltage amplitude divided by 10
−40dB Signal voltage amplitude divided by 100
Converting Between dBs and Power or Voltage gain
Table 1.3.1 Power Ratio/dB
| Power Ratio | dB |
|---|---|
| Pout/Pin | 10 log(Pout/Pin) |
| 10 000 000 000 | 100 |
| 1 000 000 000 | 90 |
| 100 000 000 | 80 |
| 10 000 000 | 70 |
| 1 000 000 | 60 |
| 100 000 | 50 |
| 10 000 | 40 |
| 1 000 | 30 |
| 100 | 20 |
| 10 | 10 |
| 4 | 6 |
| 2 | 3 |
| 1.26 | 1 |
| 1 | 0 |
| 0.79 | −1 |
| 0.5 | −3 |
| 0.25 | −6 |
| 0.1 | −10 |
| 0.01 | −20 |
| 0.001 | −30 |
| 0.000 1 | −40 |
| 0.000 01 | −50 |
| 0.000 001 | −60 |
| 0.000 000 1 | −70 |
| 0.000 000 01 | −80 |
| 0.000 000 001 | −90 |
| 0.000 000 000 1 | −100 |
Table 1.3.2 Voltage or Current Ratio/dB
| Voltage or Current Ratio | dB |
|---|---|
| Vout/Vin or Iout/Iin | 20log(Vout/Vin) 20log(Iout/Iin) |
| 100 000 | 100 |
| 31 623 | 90 |
| 10 000 | 80 |
| 3 162 | 70 |
| 1 000 | 60 |
| 316.23 | 50 |
| 100 | 40 |
| 31.623 | 30 |
| 10 | 20 |
| 3.162 | 10 |
| 2 | 6 |
| 1.414 | 3 |
| 1.122 | 1 |
| 1 | 0 |
| 0.891 | −1 |
| 0.707 | −3 |
| 0.5 | −6 |
| 0.316 2 | −10 |
| 0.1 | −20 |
| 0.031 62 | −30 |
| 0.01 | −40 |
| 0.003 162 | −50 |
| 0.001 | −60 |
| 0.000 316 2 | −70 |
| 0.000 1 | −80 |
| 0.000 0316 2 | −90 |
| 0.000 01 | −100 |


