Module 2.5
Crystal Sine Wave Oscillators
- After Studying this section, you should be able to:
- • Understand the need for Frequency control in LC Oscillators.
- • Understand the application of Quartz Crystals in LC Oscillators.
- • Understand the operation of Quartz Crystals.
- • Understand the application of Quartz Crystals in both serial and parallel modes.
- • Recognise Integrated Crystal Oscillator Modules.
Crystal Sine Wave Oscillators
Where good frequency stability is required, in applications such radio transmitters, basic LC oscillators cannot guarantee to hold their frequency without some drifting, which can be caused by quite small changes in supply voltage (although stabilised power supplies help avoid this) and changes in temperature.
The effects of resistance and stray capacitance within the circuit can also cause the oscillator to operate at a slightly different frequency from that calculated using just the values of L and C. In most cases this can be overcome by making the tuned ‘tank’ circuit have as high a Q factor as possible. With ordinary inductors and capacitors, Q factors more than a few hundred are not possible, but by using quartz crystals Q factors well in excess of 10,000 can be achieved.
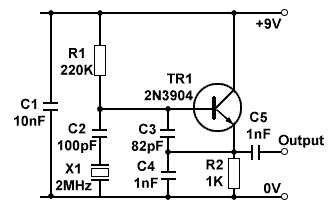
Fig. 2.5.1 Colpitts Oscillator using
a Crystal in Parallel Mode
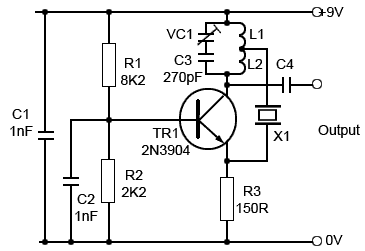
Fig. 2.5.2 Hartley Oscillator using
a Crystal in Series Mode
Crystals may be used increase frequency stability in RF oscillators such as Hartley and Colpitts. The crystal may be used either in ‘parallel mode’ e.g. as an inductor operating at a frequency between ƒ1 and ƒ2 as part of the resonating tuned circuit, as shown in the crystal controlled Colpitts oscillator in Fig 2.5.1, or in ‘series mode’ where the crystal is acting as a highly selective low impedance at ƒ1 in the feedback path as shown in a Hartley oscillator in Fig. 2.5.2.
The Quartz Crystal
The quartz crystal is a piezo-electric device, and will both produce a voltage across it when it is subjected to some mechanical distortion such as slight bending, or will distort slightly when a voltage is applied across it. Therefore applying regular voltage pulses will cause the crystal to bend, and the bending will in turn create voltage pulses in phase with the applied pulses, that will reinforce them and cause oscillation.
The frequency at which this reinforcing effect occurs is the resonant frequency of the crystal, and this is determined by the physical size of the crystal and by the way the crystal is cut in relation to its atomic structure. When a quartz crystal is accurately cut and prepared, it is almost perfectly elastic. This means that once oscillations start, they take a long time to die away.
Fig 2.5.3 shows the circuit (schematic) symbol for a quartz crystal and its equivalent circuit. Notice that in effect it contains all of the properties (L, C and R) normally associated with a tuned circuit. It can therefore be used to replace either a series tuned circuit or a parallel tuned circuit, and the graph of its impedance (Z) shows two resonant frequencies ƒ1 and ƒ2. When used in series mode the crystal exhibits very low impedance at ƒ1, and in parallel mode, a very high impedance at ƒ2. In practice, because of the extremely narrow bandwidth caused by the crystal’s very high Q factor, these frequencies are close enough together to be considered the same for many purposes.
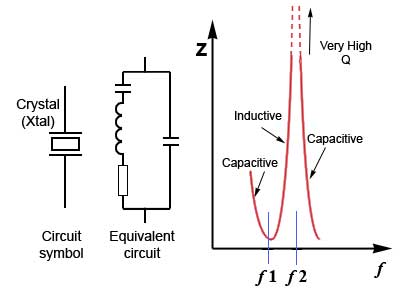
Fig. 2.5.3 The Quartz Crystal
Crystal oscillators can produce either sine wave or square wave outputs over a very wide range of frequencies, usually from one or two MHz up to several hundred MHz. Crystals are produced to resonate at many different specific frequencies for particular applications, but the range of available frequencies is made much greater by various techniques such as frequency division, where the frequency of a crystal oscillator is sequentially divided by 2 many times by digital dividers, to a much lower frequency. Because any slight errors are also reduced by the same division process, the final low frequency is much more accurate.
Crystals can also be made to resonate at higher multiples of their basic resonant frequency. One of these higher multiples, called overtones) can then be selected using a conventional LC circuit. By using these frequency division and overtone techniques a much wider range of crystal frequencies can be achieved.
Integrated Crystal Oscillator Modules
In modern circuitry it is far less common to find crystal oscillators constructed from discrete components, as many ready-made crystal oscillators are available. Both square wave and sine wave oscillators are available as DIL (dual in line) or SMT (surface mount) modules with a wide variety of specifications and frequencies.

Fig. 2.5.4 14pin DIL Crystal
Oscillator Module
In sine wave oscillators for use in radio transmission, the oscillator is the source of the transmitted radio wave, so frequency accuracy and stability are of vital importance as radio bands are usually crowded with many transmitters operating in a given radio band. Transmitters therefore must not allow their transmission frequency to wander and interfere with adjacent transmissions. Receivers must be able to tune to known reliable frequencies.
Many crystal oscillators are capable of maintaining their set frequency to within a few parts per million e.g +/- 5 to 50Hz for each MHz of their intended frequency, over temperature ranges typically from 0 to 70 degrees for consumer applications and -85 to +85 degrees for some military and aerospace specifications.
Very low harmonic distortion is also an important factor. That is, the oscillator must not output frequencies at harmonics of the design frequency, as these would create extra transmissions at these frequencies. To avoid harmonic distortion, the sine wave must be as pure as possible and oscillators are available with a total harmonic distortion (the percentage of power in generated harmonics compared to the power generated in the fundamental sine wave) of just a few percent.
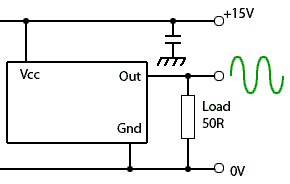
Fig. 2.5.5 Typical Oscillator
Module Connections
Many oscillator modules have only 3 pins for +Vcc Ground and output, though some have extra pins for control options and typically drive loads such as 50 ohms with an output of 500mV to 1V as shown in Fig. 2.5.5.
Because many of the characteristics of an oscillator vary with temperature, special oven controlled crystal oscillators (OCXOS) are made for the most critical applications. These oscillators are contained within a heated, thermostatically controlled case, so that in operation their temperature is kept at a constant level. This allows frequency variations to be kept typically below 1 part per million and harmonic distortion to less than 1%.


