Module 2.3
The Colpitts Oscillator
- After Studying this section, you should be able to:
- • Understand the operation of a Common Base Colpitts Oscillator.
- • Understand the operation of a Common Emitter Colpitts Oscillator.
- • Understand the need for Output Buffering.
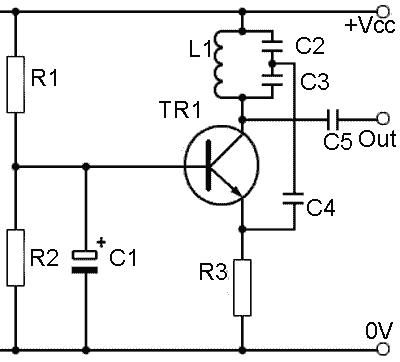
Fig. 2.3.1 The Common Base Colpitts Oscillator
Common Base Colpitts Oscillator
Fig. 2.3.1 shows a typical Colpitts oscillator design. This circuit is very similar in operation to the Hartley oscillator described in Oscillators Module 2.1 but the Colpitts LC tank circuit consists of a single inductor and two capacitors. The capacitors form in effect, a single 'tapped' capacitor instead of the tapped inductor used in the Hartley. The values of the two capacitors (connected in series) are chosen so their total capacitance in series(CTOT), is given by:
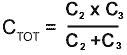
This gives the total capacitance necessary for the tank circuit to achieve parallel resonance at the required frequency. The frequency of oscillation is given by the same formula as for the Hartley oscillator:
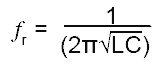
But here the value C is the calculated value of C2 and C3 in series (CTOT).
The individual values of C2 and C3 are chosen so that the ratio of the values produces the necessary proportion of feedback signal. However, the ratio of voltages across two capacitors in series is in inverse proportion to the ratio of the values, i.e. the smaller capacitor has the larger signal voltage across it. The main advantage of the Colpitts arrangement, is that the single inductor in the tuned circuit removes the effect of any mutual inductance between two coils where the alternating magnetic field built up around one inductor induces a current into the their inductor. This would affect the total inductance of the coils and so changes the resonant frequency of the tuned circuit.
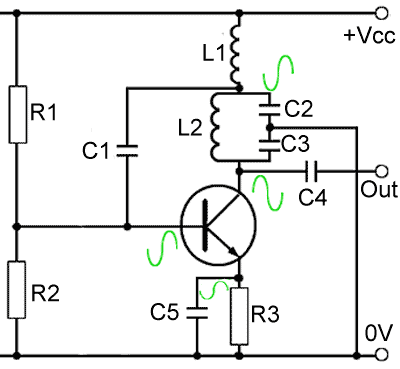
Fig. 2.3.2 A Colpitts Oscillator using
a Common Emitter Amplifier
Common Emitter Colpitts Oscillator
The circuit in Fig. 2.3.2 is the Colpitts equivalent of the Common Emitter Hartley Oscillator described in Oscillators Module 2.1 (Fig.2.1.4). It uses a common emitter amplifier, and as the tuned (tank) circuit tapping point in this configuration is connected to ground, the tank circuit produces anti-phase waves at top and bottom of L2, which ensures the correct phase relationships for positive feed back between collector and base. The feedback is applied to the base via C1, which also acts as a DC block, preventing the higher voltage on L1 upsetting the base bias voltage.
Note that the tank circuit (L2, C2 and C3)is connected to the supply rail (+Vcc) via L1. If the tank circuit were connected directly to the supply there could be no anti-phase AC signal present at the top of the tank circuit, due to the DC supply being heavily decoupled by large capacitors in the DC Ppower supply. An RF choke (L1) having a high impedance at the frequency of oscillation is therefore included between the tuned circuit and the supply. This allows for a signal voltage for feedback purposes to be developed across L1.
Automatic class C bias is used, with the emitter in this circuit only partially decoupled by a small value of C5 to give the ‘sliding bias’ previously described.
The Colpitts oscillator, like the Hartley is capable of giving an excellent sine wave shape, and also has the advantage of better stability at very high frequencies. It can be recognised by always having a "tapped capacitor"
Remember:
HartLey = tapped L
Colpitts = tapped C
Sine wave oscillator design is complicated by the fact that any load placed on the output, by circuits that the output is supplying, effectively places a damping resistance across the tank circuit. As well as reducing the amplitude of the oscillator output by having the effect of reducing the Q factor of the tuned tank circuit, this can adversely affect both the wave shape and the frequency stability of the oscillator waveform.
Buffered Colpitts Oscillator
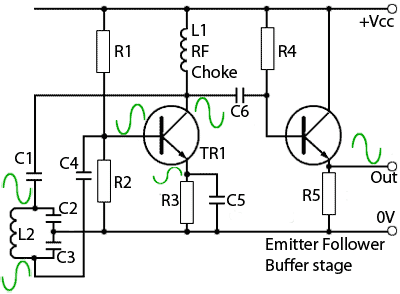
Fig. 2.3.3 Colpitts Oscillator with Buffer Stage
A common solution is to feed the oscillator output into an emitter follower buffer amplifier, as shown in Fig. 2.3.3. The oscillator section of this circuit is a slightly different version of the Colpitts oscillator in shown in Fig. 2.3.1.
The RF choke is now the load impedance for TR1 and the tank circuit is isolated from TR1 by two DC blocking capacitors, C1 and C4. Therefore this version of the Colpitts oscillator uses a tuned feedback path (Method 1 in Oscillators Module 1.1) rather than a tuned amplifier (Method 2) as in Fig. 2.3.1
The emitter follower stage (R4, TR2 and R5) has a very high input impedance, thus having little loading effect on the oscillator, and a very low output impedance allowing it to drive loads of only a few tens of ohms impedance.
The frequency stability of oscillators can also be affected by variations in supply voltage. It is common therefore, where good frequency stability is required, to use a stabilised power supply. Oscillator supplies may also need extra decoupling capacitors to remove unwanted 'noise' from the supply. Stable amplitude is normally achieved by using automatic class C bias, provided in this circuit by only partially decoupling the emitter of TR1 by C5.


