Module 4.1
BJT Astable Multivibrators
- After Studying this section, you should be able to:
- • Recognise BJT astable multivibrator circuits.
- • Understand the operation of astable multivibrators.
- • Calculate the frequency of an astable multivibrator.
- • Understand methods for varying the frequency and mark to space ratio of the output wave.
BJT Astable Multivibrators
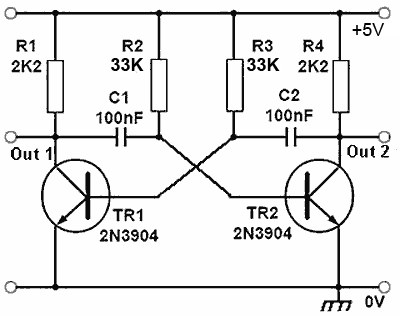
Fig. 4.1.1 Basic BJT Astable Multivibrator
The basic bipolar transistor (BJT) version of an astable multivibrator as shown in Fig. 4.1.1 has two outputs that repeatedly change state at a rate determined by the time constants of its feedback network. Although largely superseded by its equivalent op amp or timer IC versions in many applications, it is still a useful and flexible design for square wave and pulse generation. The circuits shown on this page will operate from a DC supply between 3.3V and 9V. Whilst the voltages and waveforms in the operational descriptions refer to the circuit working from a 9V supply, this supply voltage may be a little high as the base/emitter voltages on the transistors produces negative going spikes on each cycle of about -8.4V (see Fig. 4.1.3) and the data sheet for the 2N3904 specifies a maximum base/emitter voltage of 6V. Therefore a 5V supply can be recommended for greater reliablity.
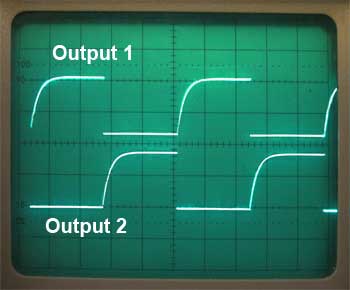
Fig. 4.1.2 Antiphase Outputs
The circuit switches continuously from one state (TR1 on and TR2 off) to the other (TR1 off and TR2 on) and back again at a rate determined by the RC timing components Cl/R2 and C2/R3. The circuit produces two anti-phase square wave signals, with an amplitude almost equal to its supply voltage, at its two transistor collectors as shown in Fig 4.1.2.
Astable Operation
Suppose that at switch on, TR1 is conducting heavily and TR2 is turned off. The collector of TR1 will be almost at zero volts as will the left hand plate of C1. Beause TR2 is turned off at this time, its collector will be at supply voltage and its base will be at almost zero potential, the same as TR1 collector, because C1 is still un-charged and its two plates are at the same potential.
C1 now begins to charge via R2 and its right hand plate becomes increasingly positive until it reaches a voltage of about +0.6V. As this plate of the capacitor is also connected to the base of TR2, this transistor will begin to conduct heavily. The rapidly increasing collector current through TR2 now causes a voltage drop across R4, and TR2 collector voltage falls, causing the right hand plate of C2 to fall rapidly in potential.
It is the nature of a capacitor that when the voltage on one plate changes rapidly, the other plate also undergoes a similar rapid change, therefore as the right hand plate of C2 falls rapidly from supply voltage to almost zero, the left hand plate must fall in voltage by a similar amount.
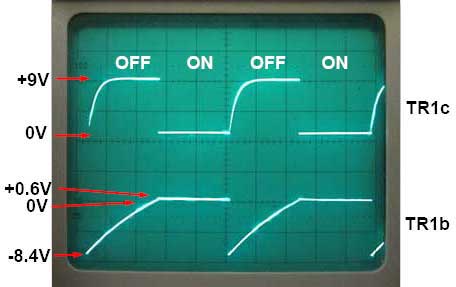
Fig. 4.1.3 Switching Action (on TR1)
With TR1 conducting, its base would have been about 0.6V, so as TR2 conducts TR1 base falls to 0.6 −9V = −8.4V, a negative voltage almost equal and opposite to that of the +9V supply voltage.
This rapidly turns off TR1 causing a rapid rise in its collector voltage. Because a sudden voltage change on one plate of a capacitor causes the other plate to change by a similar amount, this sudden rise at TR1 collector is transmitted via C1 to TR2 base causing TR2 to rapidly turn on as TR1 turns off. A change of state has occurred at both outputs.
This new state does not last however. C2 now begins to charge via R3, and once the voltage on the left hand plate (TR1 base) reaches about +0.6V another rapid change of state takes place. This switching action produces the collector and base waveforms shown in Fig. 4.1.3.
Frequency Calculations
The circuit keeps on changing state in this manner producing a square wave at each collector. The frequency of oscillation can be calculated, as the time for the relevant capacitor to charge sufficiently for a change of state to take place, will be approximately 0.7CR and, as two changes of state occur in each cycle the periodic time T will be:
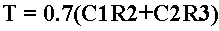
If C1 = C2 and R2 = R3 the mark to space ratio will be 1:1and in this case the frequency of oscillation will be:
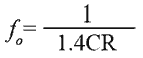
Example
What is the frequency of an astable multivibrator of mark/space ratio 1:1 using timing components of C=100nF and R=33K?
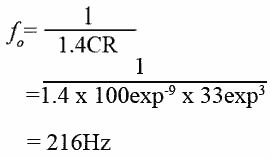
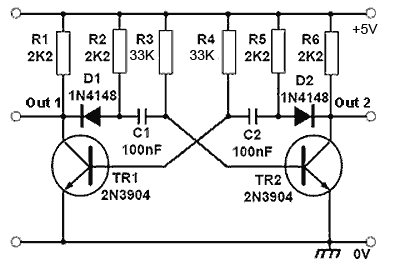
Fig. 4.1.4 BJT Astable Modified
for Improved Rise Time
A problem with the basic astable circuit is that the capacitor action described above slows down the rise in voltage as each transistor turns off, producing the curved rising edges to the square wave as can be seen in Fig. 4.1.2. This can be overcome by the modified circuit shown in Fig. 4.1.4
Each time TR2 collector voltage goes high as the transistor turns off, D2 becomes reverse biased, isolating TR2 from the effect of C2 charging. The charging current for C2 is now supplied by R5 instead of R6. The action of TR1 during its ‘off’ period is similar.

Fig. 4.1.5 Astable Output
Showing Improved Rise Time
The output waveforms at the collectors of TR1 and TR2 shown in Fig. 4.1.5 demonstrate the improved rise times achieved by the modified circuit of Fig. 4.1.4, compared with those for the basic BJT astable circuit shown in Fig. 4.1.2.
Variable Frequency Astable
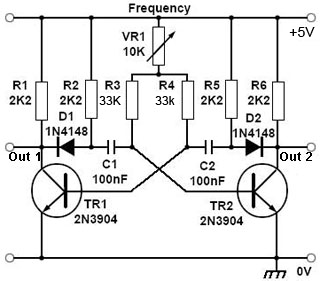
Fig. 4.1.6 Variable Frequency BJT Astable
It is useful to be able to vary the frequency of operation, and this may be done as shown in Fig.4.1.6.
By varying VR1 the voltage at the top of both R3 and R4 is varied so that whatever mark to space ratio is used, only the frequency alters, whilst the mark to space ratio is maintained.
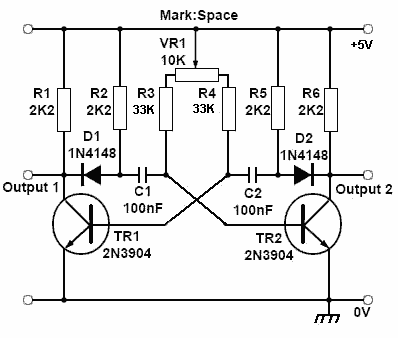
Fig. 4.1.7 Variable Mark to Space Ratio Astable
Variable Mark to space Ratio
Fig. 4.1.7 shows how by using a potentiometer instead of a variable resistor, an astable with a degree of variable mark to space ratio can be achieved.


