Google Ads
Module 9.2
Series Resonance
- Describe LCR Series Circuits at resonance.
- • Describe the conditions for series resonance.
- • Carry out calculations on LCR series circuits, involving reactance, impedance, circuit voltages and current.
Series Resonance happens when reactances are equal.
Inductive reactance (XL) in terms of frequency and inductance is given by:
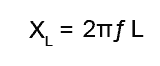
and capacitive reactance (XC) is given by:
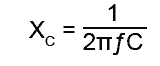
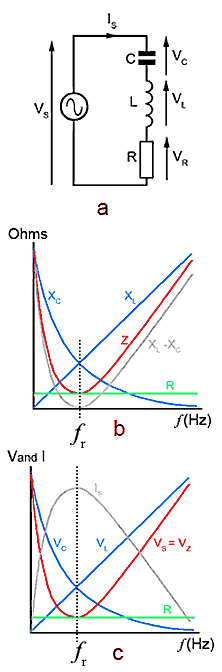
Fig 9.2.1 The Electrical Properties of a Series LCR Circuit at Resonance.
Inductive reactance is directly proportional to frequency, and its graph, plotted against frequency (ƒ) is a straight line.
Capacitive reactance is inversely proportional to frequency, and its graph, plotted against ƒ is a curve. These two quantities are shown, together with R, plotted against ƒ in Fig 9.2.1 It can be seen from this diagram that where XC and XL intersect, they are equal and so a graph of (XL − XC ) must be zero at this point on the frequency axis.
Electrical Properties of a Series LCR Resonant Circuit (Fig. 9.2.1)
Fig 9.2.1a shows a series LCR circuit and Fig 9.2.1b shows what happens to the reactances (XC and XL), resistance (R) and impedance (Z) as the supply (VS) is varied in frequency from 0Hz upwards. At first the circuit behaves as a capacitor, the total impedance of the circuit (Z) falls in a very similar curve to XL − XC.
Fig 9.2.1c illustrates the relationships between the individual component voltages, the circuit impedance(Z) and the supply current (IS) (which is common to all the series components).
At a particular frequency ƒr it can be seen that XL − XC has fallen to zero and only the circuit resistance R is left across the supply. The current flowing through the circuit at this point will therefore be at a maximum. Now VC and VL are equal in value and opposite in phase, so will completely cancel each other out. Reactance is effectively zero and the circuit is completely resistive, with Z equal to R. The circuit current (IS) will be at its maximum and will be in phase with the supply voltage (VS) which is at its minimum.
As the frequency increases above this resonant frequency (ƒr) the impedance rises, and as XL is now the larger of the two reactances, the impedance curve begins to follow an increasing value more like the linear graph of XL.
At frequencies below resonance the circuit behaves like a capacitor, at resonance as a resistor, and above ƒr the circuit behaves more and more like an inductor, and the graph of XL − XC soon becomes an almost straight line.
This behaviour of a LCR Series Circuit allows for the statement of a number of useful facts about a series circuit that relate to its resonant frequency ƒr.
6 Things you need to know about LCR Series Circuits.
- 1. AT RESONANCE (ƒr) VC is equal to, but in anti-phase to VL
- 2.; AT RESONANCE (ƒr) Impedance (Z) is at minimum and equal to the RESISTANCE (R)
- 3. AT RESONANCE (ƒr) Circuit current (IS) is at a maximum.
- 4. AT RESONANCE (ƒr) The circuit is entirely resistive.
- 5. BELOW RESONANCE (ƒr) The circuit is capacitive.
- 6. ABOVE RESONANCE (ƒr) The circuit is inductive.
Two Formulae for Series Resonance.
The fact that resonance occurs when XL = XC allows a formula to be constructed that allows calculation of the resonant frequency (ƒr) of a circuit from just the values of L and C. The most commonly used formula in electronics for the series LCR circuit resonant frequency is:
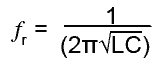
Fig 9.2.2 Deriving the Formula for Resonance
Notice that this formula does not have any reference to resistance (R). Although any circuit containing L must contain at least some resistance, the presence of a small amount of resistance in the circuit does not greatly affect the frequency at which the circuit resonates. Resonant circuits designed for high frequencies are affected by stray magnetic fields, inductance and capacitance in their nearby environment, so most high frequency LC resonant circuits will have both screening to isolate them from external effects as much as possible, and be made adjustable over a small range of frequency so they can be accurately adjusted after assembly in the circuit.
However, although this formula is widely used at radio frequencies it is often not accurate enough at low frequencies where large inductors, having considerable internal resistance are used. In such a case a more complex formula is needed that also considers resistance. The formula below can be used for low frequency (large internal resistance) calculations.
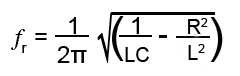
The need for careful adjustment after circuit assembly is often a deciding factor for the discontinued use of pure LC circuits in many applications. They have been replaced in many applications by solid-state ceramic filters and resonating crystal tuned circuits that need no adjustment. Sometimes however, there may be a problem of multiple resonant frequencies at harmonics (multiples) of the required frequency with solid state filters. A single adjustable LC tuned circuit may then also be included to overcome the problem.
Series Circuit Calculations.
In a series LCR circuit, especially at resonance, there is a lot happening and consequently calculations are often multi stage. Formulae for many common calculations have been described in earlier modules in this series, the difference now is that the task of finding out relevant information about circuit conditions relies on selecting appropriate formulae and using them in a suitable sequence.
For example, in the problem below, the items in values shown in red are required, but notice that VC and VL can´t be worked out first, as a value for ƒr (and another formula) is needed to calculate the reactance. Sometimes however the task is made easier by remembering the 6 useful facts about series resonance from the grey panel above. In example 9.2.2 below there is no need to calculate VL because, at resonance XC and XL are equal, and so will have equal voltages developed across them. Notice however that VL is not the same as the total voltage measured across L. The voltage across the internal resistance (at 90° to VL) needs to be included, and because of the phase difference between VL and the internal resistance voltage (V RL), the total measurable inductor voltage VL TOT will be the phasor sum of VL and V RL
Example 9.2.2 Series LCR Circuit Calculations.
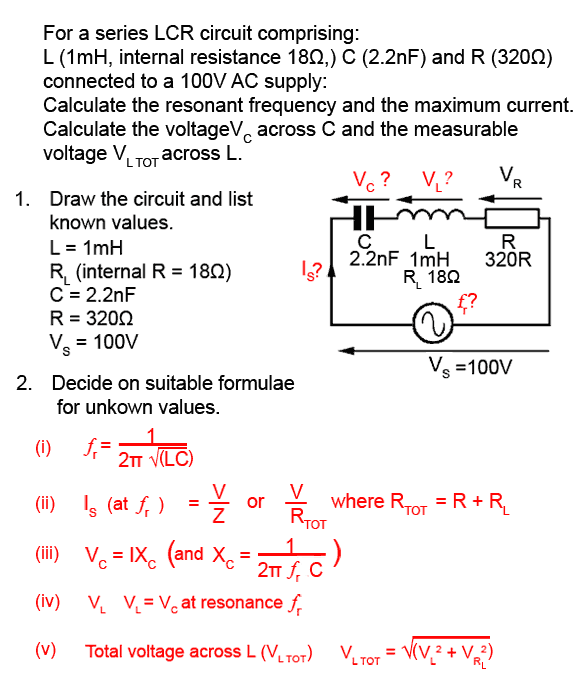
Work out each of these formulae (with pencil and paper and a calculator) remembering to work out the bracketed parts of the formula first, then check your answers in Module 9.3
Working this way while learning is a good way to help understand how the maths work. There are of course a good many LCR calculators on the web but take a tip, WORK IT OUT FIRST, then try a web calculator (or more than one, as some are cleverer than others) to check your answer.


