Google Ads
Module 1.1
AC Waves
- Module 1.1 AC Waves.
- • Fundamental & harmonic content of waves.
- • Describe a sine wave.
- • Recognise basic complex waveforms.
- • Square wave.
- • Triangular wave.
- • Sawtooth wave.
- • Recognise basic complex waveforms.
- • Recognise harmonic distortion.
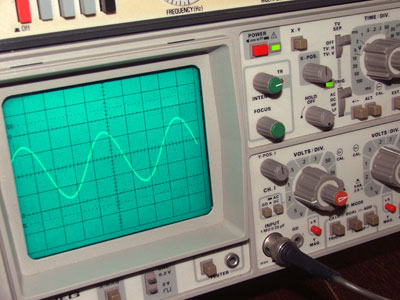
Fig 1.1.0 An Oscilloscope Displaying a Sine Wave.
What are Waves?
Information is passed from one place, or person, to another in many different ways. Whatever way information is carried, the SIGNAL used takes the form of waves. These may be sound waves or electromagnetic (including electrical or light) waves, and although these may be physically very different from each other they can all be represented by WAVEFORMS. A waveform is simply a graph that shows how the property described (e.g. sound or electricity), changes with time.
With many waves that concern electronics engineers, the actual wave, acting at high speeds within electronic circuitry cannot be seen in any normal way, but instruments such as the OSCILLOSCOPE, can draw graphs of these "invisible" waves, and so allow engineers to check that the wave is present, and has not been distorted in shape by the equipment under test. The oscilloscope is also used to measure a number of properties of waves, giving information on the performance of equipment.
Harmonics.
Signal waveforms having very complex shapes are often encountered in electronic equipment, but all repetitive waves, no matter how complex, can be shown mathematically to consist of a series of much simpler waves, each of which has the same shape. This wave shape is known as a SINE WAVE because its graph follows the mathematical SINE function. The shape of a sine wave is quite familiar, although not usually recognised as such, because its waveform or graph is not readily visible. The swinging pendulum of a clock traces out a sine wave, and many naturally occurring vibrations are SINUSOIDAL (that is "of a sine wave shape")
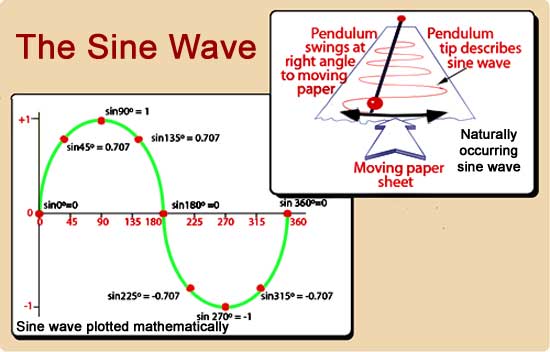
Fig 1.1.1 Sine Waves.
Sine Waves
Fig 1.1.1 shows examples of sine waves, plotted mathematically over a series of calculated points (bottom left). A sine wave can also be produced naturally (top right), by fixing a container such as a salt shaker to the end of a swinging pendulum, and moving a sheet of coloured paper at a constant speed beneath it as it swings and deposits its salt. The result is a beautiful sine wave!
The sine wave therefore is a mathematical function and a naturally occurring shape, it is also the basis of many other wave shapes and is therefore the most important waveform in the study of AC theory.
Complex Waves.
Other important wave forms commonly encountered in electronics are;
- • The Square wave:
- • The Triangular wave:
- • The Saw-tooth wave:
A complex wave is a wave made up of a series of sine waves; it is therefore more complex than a single pure sine wave. This series of sine waves always contains a wave called the "FUNDAMENTAL", that has the same FREQUENCY (repetition rate) as the COMPLEX WAVE being created.
As well as the fundamental, a complex wave contains a series of HARMONICS. These are sine waves which have frequencies that are WHOLE NUMBER MULTIPLES of the fundamental; that is, the fundamental x 2, the fundamental x 3 etc. The fundamental and the harmonics are called the COMPONENTS of a complex wave. One further component is often present in a complex wave, that is a D.C. COMPONENT. this is a component "wave" whose frequency is ZERO, i.e. it is not really a wave but merely a DC value which affects the resultant complex wave. Square, Triangular and Saw-tooth waves can be shown to consist of a fairly straightforward series of components, you should remember which series of harmonics makes up which of these three complex waves.
Square Waves
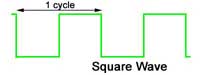
The square wave contains a fundamental and a series of ODD HARMONICS; that is harmonics which are odd number multiples of the fundamental (x3 x5 x7 etc.) These are called the 3rd harmonic, 5th harmonic etc.
Triangular Waves
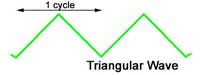
The triangular wave also contains a fundamental and a series of ODD HARMONICS, but in this case, each successive harmonic component starts off in the opposite PHASE to the previous one. i.e. the 3rd harmonic starts by going positive, the 5th harmonic begins by going negative, the 7th positive and so on. This phase change of alternate harmonics is the only difference from the square wave components, whose harmonics all start in a positive direction, yet the resultant waves are completely different.
Sawtooth Waves
The sawtooth wave contains a fundamental and both ODD and EVEN HARMONICS. In each of the above cases, the fundamental and just a few harmonic components will give the resultant wave an approximate shape to the ideal waveforms illustrated. The more harmonics included in the complex wave series, the better complex wave-shape is produced, nearer to a perfect square, triangular or sawtooth shape.
This fact is important in equipment such as hi−fi amplifiers because complex shape of the waveform at the system´s input, the waveform at the loudspeaker should ideally be exactly the same shape as the input waveform - so the sound produced is as close to the original as possible. This means that it is necessary to reproduce every sine wave component of the original wave accurately without "losing" any components on the way.
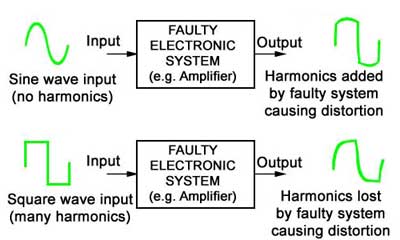
Fig 1.1.5 Harmonic Distortion
Nor should the system add any harmonics which were not in the original signal. In either case the final output signal would not be the same shape as the original and unwanted DISTORTION has been introduced into the system.
In practice however it is possible to ignore many of the harmonic components without a noticeable effect on the waveform. This is because the harmonics that are closest to the fundamental frequency (2nd, 3rd etc.) have a large amplitudes and so have a greater effect on the shape of the resultant wave, the high frequency harmonics (15th, 16th for example) are usually very small in comparison to the lower harmonics and fundamental, so they only change the resultant wave very slightly.


