Google Ads
Module 5.4
Phasor Calculations
- • Use Phasor Diagrams to Calculate Unknown Values.
- By using the following techniques:
- • Scale Drawings
- • Pythagoras´ Theorem
- • Trigonometry
Find Unknown Values Using Phasor Diagrams
There are several ways of using phasor diagrams to find out important data about LCR circuits. For example: "What supply voltage will be needed to ensure a particular voltage across the inductor in a circuit?" or "What would be the phase difference between the supply voltage and supply current at a particular frequency of operation?" and many others. Figure 5.4.1 to Figure 5.4.3 introduce three different methods of using phasor diagrams to find some unknown quantity.
Study these three methods and once you are familiar with them you can choose the best one to solve any particular problem involving the values and phase angles of AC currents and voltages in an LCR circuit.
To help you on the right track why not download our "Maths Tips" booklet, which shows you how to use your calculator to calculate angles and values using trigonometry functions and get the right answer every time.
No scientific calculator? The "Maths Tips" booklet explains what you need and don´t need from a calculator. If you don´t want to buy a scientific calculator, you can always pick up a free one from the net. PC users can try Calc98 from www.calculator.org/download.html. Whichever calculator you choose remember that you should read its instructions to become familiar with the working methods you should use as these do vary from calculator to calculator.
Method 1 Scale Drawing
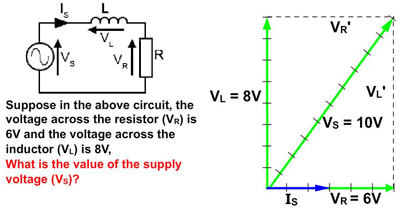
Fig. 5.4.1 Calculation by Scale Drawing
Because the components of the circuit are connected in series, IS is common to all components, so IS will be the reference phasor. It is drawn at 0° (horizontally to the right of the origin point). As the problem only requires voltages, the scale of IS does not matter.
A phasor is drawn 6 units (cm, inches etc.) long. Because both resistor current and voltage are always in phase with each other, VR is in phase with the reference phasor IS. The value is shown as VR = 6V. (the small tick marks on the phasor are only given here to show scale.)
In a pure inductor, voltage (VS) leads current (IS) by 90°, so an 8V phasor is drawn vertically from the common point of origin.
A line, the same length as, and parallel to VR is drawn from the top of VL to form the top of a rectangle (VR').
The right side of the rectangle (VL') is drawn from the tip of VR' the same length as, and parallel to (VL).
A phasor showing VS can now be drawn from the origin point, diagonally to the opposite corner of the rectangle.
The measured length of this phasor will be the phasor sum of VR and VL, which in this case will be 10V.
Method 2 Pythagoras' Theorem
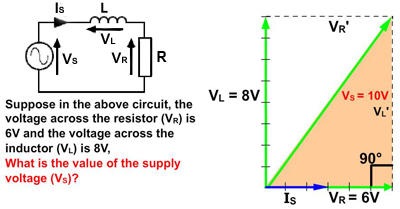
Fig. 5.4.2 Calculation by Pythagoras' Theorem
Because, in this example, the area within VS, VL and VR is a right angle triangle, the length of the Hypotenuse (VS) can be found using Pythagoras' Theorem, which states:
The square of the hypotenuse (VS in this example) of a right angle triangle is equal to the sum of the squares of the two adjacent sides (VL' and VR).
The formula:
1. VS2 = VL2 + VR2 (using the symbols from the phasor diagram in Fig. 5.4.2).
2. VS2 = 82 + 62 (replace the symbols with the known values).
3. VS2 = 64 + 36 = 100 (work out the value of VS2 ).
4. VS2 =
5. The Answer: VS = 10V (remember the units you are working in - Volts in this example).
Method 3: Using the Inverse Trigonometry Functions
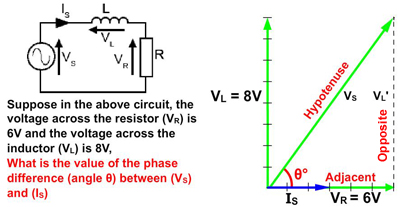
Fig. 5.4.3 The Inverse Trigonometry Functions
The formula for finding an angle depends on which sides of the triangle have a known value. The choice for finding the unknown angle Θ (in degrees) is between:
Method a: Θ° = sin-1 (Opposite / Hypotenuse)
Method b: Θ° = cos-1 (Adjacent / Hypotenuse)
Method c: Θ° = tan-1 (Opposite / Adjacent)
Even when the value of the hypotenuse (VS) is not known (as in Fig. 5.4.3), the tan-1 formula (method c) can be used to find the angle Θ
Θ° = tan-1 (Opposite / Adjacent)
Θ° = tan-1 (8/6)
Θ° = tan-1 1.333333333
Θ = 53.13° (53° would normally be near enough.)


